Wednesday, May 29, 2013
Part ll Day 7
Daily objective- Similar triangles
Deffinition- Students will be able to apply what we learned about similar triangles from day 6 to a real life sensereo.
Lets review what a similar triangle is again? Its the same idea as what we leared on day 5 and day 6. We use proportunes of similar figures to find missing lenghths.
EXSAMPLE FROM DAY 5.
This proses can be used for real life scenarios espeshaly with triangles.
Example- let's say you half to find the hight of a tree using the shadow. This sets up a perfect triangle where you can use similar triangles to find the missing side.(the hight!)
Because we know the actual high of the small tree we can find the actual high of the big tree. We follow the same proses as previous days 5and6. 3 is 1/10 30. So three is 10times 2. The tree will be 20feet tall.
-We can serenely use similar triangles and shapes in real life situations.
QUIZ-TIME!!!!!
1.) What example did I use in this post to set up a problem like this?
2.)If there's a small tree with a shadow of 10 feet and a high of 20 feet. What will the hight of a tree be if the large tress shadow is 20 feet.
3.))If there's a small tree with a shadow of 30 feet and a high of 60 feet. What will the hight of a tree be if the large tress shadow is 20 feet.
Deffinition- Students will be able to apply what we learned about similar triangles from day 6 to a real life sensereo.
Lets review what a similar triangle is again? Its the same idea as what we leared on day 5 and day 6. We use proportunes of similar figures to find missing lenghths.
EXSAMPLE FROM DAY 5.
From the information were given were able to find x. For this problem the proses would befirst making fractions. 2/8 and x/16. This means that is 8 is double 16. X would be double 2. The ANSER would be 4
This proses can be used for real life scenarios espeshaly with triangles.
Example- let's say you half to find the hight of a tree using the shadow. This sets up a perfect triangle where you can use similar triangles to find the missing side.(the hight!)
Because we know the actual high of the small tree we can find the actual high of the big tree. We follow the same proses as previous days 5and6. 3 is 1/10 30. So three is 10times 2. The tree will be 20feet tall.
-We can serenely use similar triangles and shapes in real life situations.
QUIZ-TIME!!!!!
1.) What example did I use in this post to set up a problem like this?
2.)If there's a small tree with a shadow of 10 feet and a high of 20 feet. What will the hight of a tree be if the large tress shadow is 20 feet.
3.))If there's a small tree with a shadow of 30 feet and a high of 60 feet. What will the hight of a tree be if the large tress shadow is 20 feet.
ANSWER KEY
1.) I used the high of the tree in relationship to the shadow of the tree.
2.) We see that the shadow is 1/2 the actual high from the small tree. So the high of the actual large tree will be 2xs it's shadow size. 20x2=40 the large tree will be 40feet tall.
3.)We see that the shadow is 1/2 the actual high of the tree. So the length of the small trees shadow is 2xs it's 20foot shadow. The tree will be 40feet tall.
Cheak this video out to get a review on similar figures!!!
Part II Day 8
Daily objective: Scale factor of sides and scale factor of area.
Define: Basically this is just rewording what you learned from day 2. So basically apply cross-multiplication to your area of any figure and/or side.
These two videos should help you answer, understand, and apply the lesson to real life as well as answer the questions asked in the following quiz.
QUIZ:
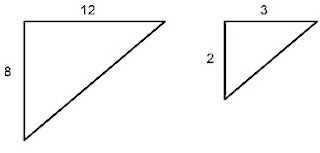
Find the scale factor for the similar figures shown below. The scale should be from the smaller figure to the larger figure.
1)
ANSWERS
1) 6/3= 2
So, the smaller figure is half of the larger figure making the scale 2.
2) 4/12 = 6/?
If you reduce the first fraction in the proportion set-up then you will have 1/3= 6/?
The purpose of reducing the fraction is to make for easier numbers.
Now cross multiply to find the missing number.
? = 18 cm squared
3) Take a number from each figure that are on the same side of the figure.
For this figure your two possible equations are 8/2 or 24/6.
When you solve (divide), you get a scale factor of 4.
Define: Basically this is just rewording what you learned from day 2. So basically apply cross-multiplication to your area of any figure and/or side.
Here is a repeat video to refresh your memory
These two videos should help you answer, understand, and apply the lesson to real life as well as answer the questions asked in the following quiz.
QUIZ:
Find the scale factor for the similar figures shown below. The scale should be from the smaller figure to the larger figure.
1)
2) Find the missing number.
3) Solve for the scale factor from the small figure to the larger figure
ANSWERS
1) 6/3= 2
So, the smaller figure is half of the larger figure making the scale 2.
2) 4/12 = 6/?
If you reduce the first fraction in the proportion set-up then you will have 1/3= 6/?
The purpose of reducing the fraction is to make for easier numbers.
Now cross multiply to find the missing number.
? = 18 cm squared
3) Take a number from each figure that are on the same side of the figure.
For this figure your two possible equations are 8/2 or 24/6.
When you solve (divide), you get a scale factor of 4.
Tuesday, May 28, 2013
Part II Day 6
State and define the daily objective in this unit: Students will be able to solve for similar triangle problems, as well as angle-angle problems.
Define: Finding the length of any side of a triangle can b simple if you have all of the measurements of one triangle as well as all of the measurements of a similar triangle but scaled in size. Similar triangles have equal angles and equivalent side lengths. When something is "scaled in size" it basically is equivalent in size, wether it is bigger in size or smaller it will always be capable of equaling the other figure using cross multiplication. Cross multiplication is a proportion made with lengths from the same side on either triangle below another pair of lengths on the same side of either triangle. When the proportion is set-up you multiply the two numbers diagonal of each other and divide by your 3rd number to find x. This is shown below.
Example: (cross-multiplication and two similar triangles)
QUIZ
For the following similar triangles find the measure of the missing length.
1)
2)
3)
ANSWERS
1) x/9=2/4 <--- proportion. Now solve for x
18/4 <--- reduce to find x
x= 4.5
2) 5/7.5 = 8/x
7.5 x 8 = 60
60/5 = 12
x= 12
3) 6/4.5= x/6
6 x 6 = 36
36/4.5 = 8
x= 8
Define: Finding the length of any side of a triangle can b simple if you have all of the measurements of one triangle as well as all of the measurements of a similar triangle but scaled in size. Similar triangles have equal angles and equivalent side lengths. When something is "scaled in size" it basically is equivalent in size, wether it is bigger in size or smaller it will always be capable of equaling the other figure using cross multiplication. Cross multiplication is a proportion made with lengths from the same side on either triangle below another pair of lengths on the same side of either triangle. When the proportion is set-up you multiply the two numbers diagonal of each other and divide by your 3rd number to find x. This is shown below.
Example: (cross-multiplication and two similar triangles)
QUIZ
For the following similar triangles find the measure of the missing length.
1)
2)
3)
ANSWERS
1) x/9=2/4 <--- proportion. Now solve for x
18/4 <--- reduce to find x
x= 4.5
2) 5/7.5 = 8/x
7.5 x 8 = 60
60/5 = 12
x= 12
3) 6/4.5= x/6
6 x 6 = 36
36/4.5 = 8
x= 8
Part ll Day 5
Daily Objective- What are similar figures, and how do you find the missing lengths to them?
Objective Definition- Students will be able to define a similar figure and find missing lengths of them.





Objective Definition- Students will be able to define a similar figure and find missing lengths of them.
DEFINITION
Similar figure- Two geometrical objects are called similar if they both have the same shape.
WHAT DEFINES A SIMILAR SHAPE?
Example 1
These two triangles are similar. We can prove that they are similar using a ratio table to compare the lengths of their corresponding sides.

Big triangle
| Small triangle |
| 20 | 15 |
| 8 | 6 |
| 16 | 12 |
- In the table, you can see that the ratio of the bases is 15/20. This reduces to
43 . - Also in the table you can see that the ratio of the two right sides is 6/8. This reduces to
43 . - Finally, the ratio of the two left sides is 12/16. This reduces to
43 .
Since all three ratios are equivalent, then the two triangles are similar.
Therefore, the two triangles are similar.
|
HOW TO FIND MISSING LENGTHS OF SIMILAR FIGURES?
Obtain the missing length if the given pair of triangles is similar.

Step 1
Label the vertices of the two similar triangles.
See the figure.

Step 2
The lengths of corresponding sides of similar figures are in proportion.
Here, the side AB corresponds to the side DE and the side BC corresponds to the side EF.
So,
Step 3
In a proportion, cross products are equal.
Write the cross products.
12 · 3 = x · 6
Step 4
Simplify both the sides. We get:
36 = 6x
Step 5
Here, x is multiplied by 6.
So, to isolate x, divide each side by 6.
Step 6
Simplify both the sides. We get:
6 = x
So, the length of the side DE is 6 in.
Here's an awesome video explaining, check it out.
QUIZ TIME KIDS!
ANSWER KEY!
1.)Because there given sides are proportional to each other. 8 is to 2 as 12 is to 3. And if you simplify both fractions 8/12 and 2/3 you get 2/3 which makes these proportional or similar shapes.
2.) 3=2 30=x(height of tree) 2/3 x/30. 2x30=60/3=20. The tree is 20 feet tall.
3.) x =....2/8 x/16...2x16/8=4. The answer is 4
Thursday, May 23, 2013
Part II Day 4
State the daily objective: Students will be able to apply the surface of prisms, pyramids, cylinders, cones, and sphere.
Define: Now that you know the formula to find all of the surface areas for the following figures, you can now understand how to apply this to real life. One example would be shingling a roof. You would need to know the surface area so you could divide the shingle's area into it to figure out how many shingles or packs of shingles you need to buy. Furthermore, if you were painting any part of your house you would need the area so that you could calculate how many cans of paint you need based on how many square feet a can covers.
 |
| Shingles |
QUIZ:
1) How many shingles do you need to order if you want to spend as little money as possible? (Bottom of the pyramid not included).
| Surface Area: Add the area of the base to the sum of the areas of all of the triangular faces. The areas of the triangular faces will have different formulas for different shaped bases. |
2)How many cans of paint do you need to buy in order to fully paint the dome shaped house? One can (gallon) of paint covers 400 square feet.
.jpeg)
| Surface = 4pr2S = 4pr2 dived in half because it is half a sphere |
.jpeg)
3) How many square feet of carpet do you need to order for your hexagonal floor?

Formula: 1/2 of the apothem x the perimeter
ANSWERS:
1) 6 x 6= 36 = bottom- not included
6 x 12= 72/2= 36
36 x 4= 144
144 sq. inches
2) 4 x 3.14 x 48 squared = 14469.12 sq. in.
3) 3/2= 1.5
1.5 x (5x6) = 45 sq. in.

Formula: 1/2 of the apothem x the perimeter
ANSWERS:
1) 6 x 6= 36 = bottom- not included
6 x 12= 72/2= 36
36 x 4= 144
144 sq. inches
2) 4 x 3.14 x 48 squared = 14469.12 sq. in.
3) 3/2= 1.5
1.5 x (5x6) = 45 sq. in.
Wednesday, May 22, 2013
Part ll Day 3
Daily objective- Surface area of a prism, pyramid, cylinder, cone and sphere.
Objective definition- Students will be able to find the surface area of given shapes and know the formulas to do so.
 Sphere
Sphere
FOR MORE INFORMATION CHECK OUT THIS VIDEO!
Objective definition- Students will be able to find the surface area of given shapes and know the formulas to do so.
FORMULAS FOR SURFACE AREA
 | Prisms Volume = Base X Height v=bh Surface = 2b + Ph (b is the area of the base P is the perimeter of the base) |
 | Pyramid V = 1/3 bh b is the area of the base Surface Area: Add the area of the base to the sum of the areas of all of the triangular faces. The areas of the triangular faces will have different formulas for different shaped bases. |
 | Cylinder Volume = pr2 x height V = pr2 h Surface = 2p radius x height S = 2prh + 2pr2 |
 | ConesVolume = 1/3 pr2 x height V= 1/3 pr2h Surface = pr2 + prs S = pr2 + prs =pr2 + pr |
 Sphere
Sphere
Volume = 4/3 pr3
V = 4/3 pr3
Surface = 4pr2
S = 4pr2
Got these pics at http://math.about.com/library/blmeasurement.htm, check it out!
NOW THAT WE KNOW THE FORMULAS, LETS PRACTICE!
QUIZ
1.)If we have a cylinder with a height of 6, and a radius of 2. What is the surface area of that cylinder?
2.)If we have another cylinder with a height of 12 and a radius of 4. What is the surface area of that cylinder?
3.)What is the forula to find the surface area of a cone?
ANSWER KEY
To find the area of the top and bottom we will do 3.14rsquared. The answer will be (after multiplying 12.566 by 2 because there is top and bottom) 25.132
Now we find the sides.. The equation 2*3.14 * r * h, so after we plug in our numbers to the equation ( 2*3.14*2*6) the answer for the 2nd part will be 75.398.
And finally we will just add the first and 2nd part together to get a total surface area of 87.964squre units.
2.) This is the same process just with different numbers. We start by putting our top and bottom circle numbers into there position in the equation 3.14rsquared. Once we complete 3.14x4sqared we multiply 50.265 by 2 because there is a top and a bottom, the answer for that step is 100.530. Next we go on the sides using the formula 2*3.14 * r * h..now we just plug in the numbers 2*3.14 * 4 *12. We get 301.592, and the final step is adding step one and step two together to get the final surface area. 301.528+100.530 and we get the ANSWER 402.122square units.
3.) pr2 + prs is the formula to find the surface area of a cone.
FOR MORE INFORMATION CHECK OUT THIS VIDEO!
Tuesday, May 21, 2013
Part II Day 2
State the daily objective: Area day 2 and introduce concept of scale (dilations).
Define: To find the area of a similar shape or scaled area you want to use cross multiplication. An example is shown below:
Here is a video to help you understand scale furthermore:
QUIZ
For the following figures find the area using the scale given
1) Scale factor= 1/2
area= 60 sq. in.
Area = x
2) Scale factor 1/6
Area = 120 sq. in.
Area = x
Define: To find the area of a similar shape or scaled area you want to use cross multiplication. An example is shown below:
Here is a video to help you understand scale furthermore:
For the following figures find the area using the scale given
1) Scale factor= 1/2
area= 60 sq. in.
Area = x
2) Scale factor 1/6
Area = 120 sq. in.
Area = x
Monday, May 20, 2013
Part ll Day 1
Daily objective- Area of squares, rectangles, triangles, trapezoids, parallelogram, circles, and polygons.
Definition- Students will be able to find the area of given shapes using my given equations and objectives.
Point- A point only respecify a location, it has no depth, nor length no width. We usually specify a point in geometry with a dot or a "point".
Definition- Students will be able to find the area of given shapes using my given equations and objectives.
VOCAB DEFINITIONS
Point- A point only respecify a location, it has no depth, nor length no width. We usually specify a point in geometry with a dot or a "point".
line- A long narrow mark or band that extends in both directions forever unless an end point is distinguished. "I drew a straight line."
Plane- A flat two dimensional surface
Line segment- A part of a line that is defined between two end points, and contains every point on the line between its end points.
Ray- A line which starts at a point with given coordinates, and goes off in a particular direction to infinity, possibly though a second point.
Angle- The space (measured in degrees) between two intersecting halves or surfaces at or close to the point where they meet.
Median- Middle value
Altitude- it it the height, or the distance from the base of a shape to the vertex
Perpendicular- A straight line at an angle of 90* to a given line, plane or surface
HOW TO FIND AREA OF DIFFERENT SHAPES
What are the formulas?
Squares- Area = width × height
Rectangles- Area= length x width
Triangles- Area = ½ × b × h
b = base h = vertical height
Trapezoid - Area= ((b1+b2)/2) h
Parallelograms-Area = b x a
b is the length of any base
a is the corresponding altitude
Circles- Area=Πr2
Polygons- Area= 1/2 Perimeter * Apothem or 1/2(PA)
1.) What will the area of a circle be given the radius is 5?
2.) What will the area be of a rectangle with a length of 4, and a width of 3?
3.) What is a median?
3.) A median is the middle value.
BELOW IS A GREAT AND SIMPLE VIDEO OF FINDING AREA, CHECK IT OUT!!
http://www.youtubehttp://www.youtube.com/watch?v=oApSNVkyTBE.
QUIZ
2.) What will the area be of a rectangle with a length of 4, and a width of 3?
3.) What is a median?
ANSWER KEY
1.) We know that the formula for finding the area of a circle is 3.14rsquared. If we plug in the numbers the the equation we come up with. 3.15 x 5squared. If the steps are followed correctly the answer will be 78.535...units squared.
2.) We know the formula for finding the area of a rectangle it length x width. Our length is 4 and our width is 3. All that's left is plugging the numbers to multiply them. 4x3=12. The area of the rectangle is 12units squared.3.) A median is the middle value.
BELOW IS A GREAT AND SIMPLE VIDEO OF FINDING AREA, CHECK IT OUT!!
http://www.youtubehttp://www.youtube.com/watch?v=oApSNVkyTBE.
Thursday, May 16, 2013
Day 4
Daily objective- Students will be able to graph linear inequalities.
Definition- Taking a linear inequality and transferring the correct information and apply it to a properly formatted graph to show given and sometimes un-given information.
What is a inequality?
- A inequality is "When the two expressions are connected by 'greater than' or 'less than' sign, we get an inequality."
EXAMPLE- When operating in terms of real numbers, linear inequalities are the ones written in the forms
Definition- Taking a linear inequality and transferring the correct information and apply it to a properly formatted graph to show given and sometimes un-given information.
What is a inequality?
- A inequality is "When the two expressions are connected by 'greater than' or 'less than' sign, we get an inequality."
EXAMPLE- When operating in terms of real numbers, linear inequalities are the ones written in the forms
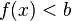 or
or  ,
,
How to graph the equation of a linear inequality
To understand how to graph the equations of linear inequalities such y ≥ x + 1, make sure that you have a good understanding of how to graph the equation of a line in slope intercept form.A linear inequality is describes an area of the coordinate plane that has a boundary line. Every point in that region is a solution of the inequality.
VERY SIMPLE!!
STEP 1-Graph it as if its an equality
STEP 2- Look at the sign, less than you shade below the line, grater than you shade the area above the line the line.
EXAMPLE-
In this case the line was shaded below the line because the equation has a less then inequality.
QUIZ!!!
2.)Now, what does the graph of y > x +3 look like?
3.)What would the graph of y ≤ -x + 1 look like?ANSWER KEY1.)Y=X+3
For another great way of looking at this, check out this video!- http://www.youtube.com/watch?v=kLfgjxmtfm8&sns=em
Subscribe to:
Comments (Atom)